General
-
Expected Tues & Thurs 10:50 -- 11:50 a.m. Email Neidinger (rineidinger) if not working or to arrange any other time.
-
The linked page will post tutor schedules for drop-in assistance, as well as links to schedule an appointment with a tutor. Located in the Center for Teaching & Learning (CTL) on the first floor of the College Library, the MSC’s drop-in hours are Sunday through Thursday, 8-11 PM, beginning Sunday, August 29. Prior to visiting for drop-in help, be sure to look at the tutor schedules to determine when an appropriate tutor for Calculus will be present.
-
Students can ask any questions about the course here.

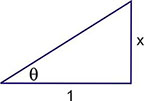 , find sin
, find sin